abc-397 题解

C - Variety Split Easy

题目大意

给定一个长度为 $N$ 的整数序列： $A = (A_1, A_2, \dots, A_N)$ 。

将 $A$ 分成两个非空的连续子数组，求这两个子数组中不同整数的个数之和的最大值。

更正式地，给定一个整数 $i$ ，其中 $1 \leq i \leq N-1$ ，要求求出如下两个值的和的最大值：

子数组 $(A_1, A_2, \dots, A_i)$ 中不同整数的个数。
子数组 $(A_{i+1}, A_{i+2}, \dots, A_N)$ 中不同整数的个数。

Constraints

$2 \leq N \leq 3 \times 10^5$
$1 \leq A_i \leq N$ ( $1 \leq i \leq N$ )
All input values are integers.

思路

可以用两个数组 pre 和 bak s分别表示从 $1 \sim i$ 子段不同整数个数之和和从 $i \sim n$ 子段不同整数个数之和。

通过上面的预处理, 我们便可以快速得知每个切割位置得到两个子段中不同整数个数和, 因此, 遍历每个可切割位点, 更新答案即可。

CODE

void solve()
{
    int n;  cin >> n;
    vector<int> v(n + 1);
    for (int i=1;i<=n;i++)  cin >> v[i];

    vector<int> pre(n + 2, 0), bak(n + 2, 0), mmap(n + 2, 0);
    for (int i=1;i<=n;i++)
    {
        pre[i] = pre[i - 1] + (!mmap[v[i]]);
        mmap[v[i]] ++;
    }
    mmap.assign(mmap.size(), 0);
    for (int i=n;i>=1;i--)
    {
        bak[i] = bak[i + 1] + (!mmap[v[i]]);
        mmap[v[i]] ++;
    }

    int ans = 0;
    for (int i=1;i<n;i++)
        ans = max(ans, pre[i] + bak[i + 1]);
    cout << ans << _endl;
}

E - Path Decomposition of a Tree

题目描述

给定一棵包含 $NK$ 个顶点的树。顶点编号为 $1,2,\dots,NK$ ，第 $i$ 条边（ $i=1,2,\dots,NK-1$ ）双向连接顶点 $u_i$ 和 $v_i$ 。

判断是否可以将这棵树分解为 $N$ 条长度为 $K$ 的路径。更确切地说，判断是否存在一个 $N \times K$ 的矩阵 $P$ 满足以下条件：

数列 $P_{1,1}, P_{1,2}, \dots, P_{1,K}, P_{2,1}, \dots, P_{N,K}$ 是 $1,2,\dots,NK$ 的一个排列。
对于每个 $i=1,2,\dots,N$ 和 $j=1,2,\dots,K-1$ ，存在一条边连接顶点 $P_{i,j}$ 和 $P_{i,j+1}$ 。

你需要判断是否存在这样的矩阵 $P$ 。

Constraints

$1 \leq N$
$1 \leq K$
$NK \leq 2 \times 10^5$
$1 \leq u_i < v_i \leq NK$
The given graph is a tree.
All input values are integers.

思路

要想将所有点分为 $N$ 条长度均为 $K$ 的路径，即需从某一点 dfs 至图的最深层，

当 dfs 回归时，对于以一点为根的子树，记其包含的点为 $T$ .

若 $T\ ==\ k$ , 分析其子节点数 $S$ ：当 $S > 2$ 时，则无法形成一条路径；只有当 $S \leq 2$ 时, 才可形成路径。

（下图要求 $k == 4$ ）

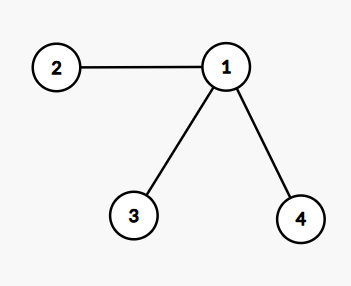
若 $T < k$ , 若 $S \geq\ 2$ , 则无法形成一条路径（由于已经是递归的返程，无法在这一子树中新增节点）。

（下图要求 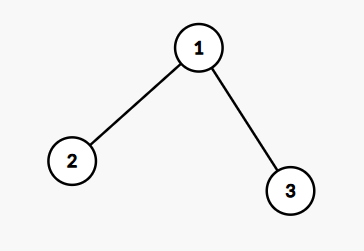$k == 4$ ）

若 $T > k$ , 无法形成。

分析样例一， $N = 3$ , $K = 2$ , 可将六个点分为如下图的三条路径。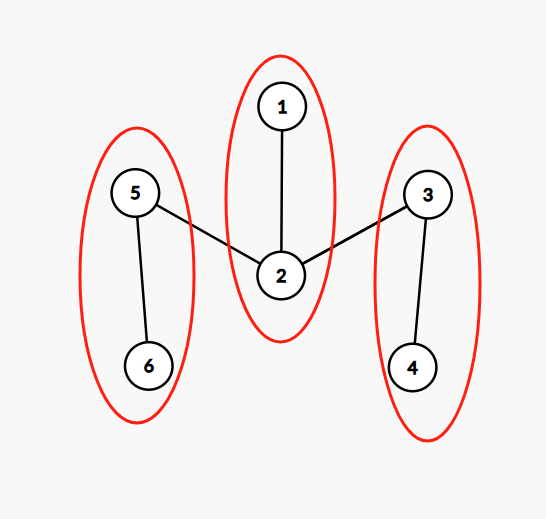

分析样例二， $N = 3$ , $K = 2$ , 对于节点 $3$ , 无论其选择与节点 $4$ 或节点 $6$ 形成路径，都会将另一点隔绝。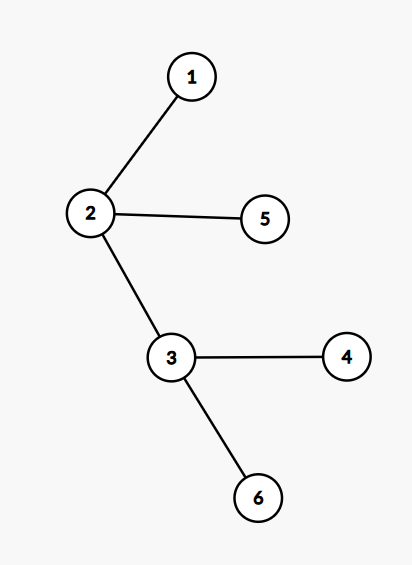

CODE

void EXIT() {cout << "No";	exit(0);};

void solve()
{
    int n, k;   cin >> n >> k;
    vector<vector<int>> adj(n * k + 1);
    for (int i=1;i<n*k;i++)
    {
        int u, v;   cin >> u >> v;
        adj[u].push_back(v);
        adj[v].push_back(u);
    }

    vector<int> siz(n * k + 1);
    auto dfs = [&](auto self, int u, int f) -> void 
    {
        siz[u] = 1;
        int son = 0;
        for (auto s : adj[u])
        {
            if (s == f) continue;
            self(self, s, u);
            if (siz[s])
                son ++, siz[u] += siz[s];
        }

        if (siz[u] == k && son <= 2)
        	siz[u] = 0;
        else if (siz[u] == k && son > 2)
            EXIT();
        else if (siz[u] < k && son > 1)
   			EXIT();
        else if (siz[u] > k)
            EXIT();
    };

    dfs(dfs, 1, 0);
    cout << "Yes";
}

F - Variety Split Hard

题目大意

给定一个长度为 $N$ 的整数序列： $A = (A_1, A_2, \dots, A_N)$

将 $A$ 分成三个非空的连续子数组，求这三个子数组中不同整数的个数之和的最大值。

更正式地，给定一对整数 $(i, j)$ ，其中 $1 \leq i < j \leq N-1$ ，要求求出如下三个值的和的最大值：

子数组 $(A_1, A_2, \dots, A_i)$ 中不同整数的个数。
子数组 $(A_{i+1}, A_{i+2}, \dots, A_j)$ 中不同整数的个数。
子数组 $(A_{j+1}, A_{j+2}, \dots, A_N)$ 中不同整数的个数。

Constraints

$3 \leq N \leq 3 \times 10^5$
$1 \leq A_i \leq N$ ( $1 \leq i \leq N$ )
All input values are integers.

思路

类似于 C 题的思路, 预处理出 pre (从 $1 \sim i$ 子段不同整数个数之和) 和 bak (从 $i \sim n$ 子段不同整数个数之和) 数组。

接下来，我们面临的问题是：在 C 题中，只有一个切割点，我们可以在 $\mathcal O(n)$ 的时间内求得答案。但是本题中，存在两个位置的切割点， $\mathcal O(N^2)$ 的时间复杂度，难以快速求解答案，无法满足我们的需求。

我们需要先固定一个切割点(右切割点)：

记中间子段不同整数个数的和为 f(l, r)

因此，题目转化为了求

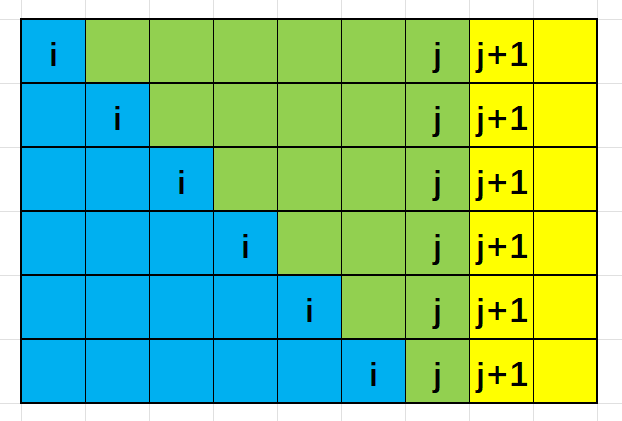
\max\limits_{j\in[2, n-1]} \{pre_1 + f(2,j),\ pre_2 + f(3, j),\ pre_3+f(4, j),\ \dots\ ,\ pre_{j-1}+f(j,j)\} \\ +\ bak_{j+1}

观察上面的式子，当 $j$ 变为 $j+1$ 时，

若 $v[j + 1]$ 存在于中间子段，则其加入无法对中间子段的不同整数的个数产生贡献。

而当 $v[j + 1]$ 不存在于中间子段时，则其加入将对中间子段不同整数个数产生贡献。

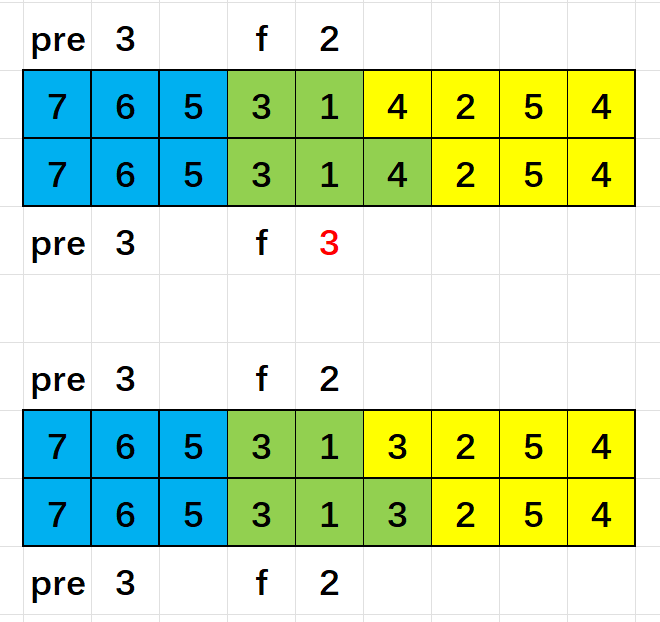
因此，我们需要记录当前位置的 $v_i$ 上一次出现的位置 (若前面未曾出现，则为 $0$ ) 。因此定义 lst 数组记录我们所需信息。

我们再看回 $pre_1 + f(2,j),\ pre_2 + f(3, j),\ pre_3+f(4, j),\ \dots\ ,\ pre_{j-1}+f(j,j)$ 序列：（将 pre 简称为 p）

p_1 + f(2,j)\qquad p_2 + f(3, j)\qquad p_3+f(4, j)\qquad \dots\qquad p_{j-1}+f(j,j) \\ p_1 + f(2,j+1)\quad p_2 + f(3, j+1)\quad p_3+f(4, j+1)\quad \dots \quad p_{j-1}+f(j,j+1) \\ p_{j}+f(j+1,j+1)

可以发现，不仅仅是 f(l, r) 右边界扩展了，序列还增加了一项 $pre_{j}+f(j+1,j+1)$ 。

f(l, r) 右边界扩展当且仅当 $v[j + 1]$ 不存在于中间子段时，其加入会对中间子段不同整数个数产生贡献。即区间 $[lst_{j+1} + 1, j]$ 中间子段不同整数个数会加一。

总结一下我们的需求：一个能够快速实现区间修改（处理贡献），区间查询最值（更新答案）的数据结构 —— 线段树！！

CODE

struct Laz
{
    int add = 0;
    void apply(const Laz &tag)
    {
        if (tag.add)
            add += tag.add;
    }
};

struct Info
{
    int mx = 0;
    Info() {}
    Info(int x) : mx(x) {}
    void apply(const Laz &tag, int len)
    {
        if (tag.add)
            mx += tag.add;
    }

    Info operator+ (const Info &a) const
    {
       Info res;
       res.mx = max(mx, a.mx);
       return res;
    }
};

void solve()
{
    int n;  cin >> n;
    vector<int> v(n + 1);
    for (int i=1;i<=n;i++)  cin >> v[i];
    vector<int> pre(n + 2, 0), bak(n + 2, 0), lst(n + 2, 0), mmap(n + 2, 0);
    for (int i=1;i<=n;i++)
    {
        pre[i] = pre[i - 1] + (!mmap[v[i]]);
        lst[i] = mmap[v[i]];
        mmap[v[i]] = i;
    }
    mmap.assign(mmap.size(), 0);
    for (int i=n;i>=1;i--)
    {
        bak[i] = bak[i + 1] + (!mmap[v[i]]);
        mmap[v[i]] = i;
    }

    int ans = 0;
    SegTree<Info, Laz> seg(n);
    for (int j=1;j<=n;j++)
    {
        seg.modify(j, j, {pre[j - 1]});
        seg.modify(lst[j] + 1, j, {1});
        ans = max(ans, seg.query(1, j).mx + bak[j + 1]);
    }
    cout << ans << _endl;
}

G - Maximize Distance

题目描述

给定一个有向图，包含 $N$ 个顶点和 $M$ 条边。顶点编号为 $1, 2, \dots, N$ 。第 $j$ 条边（ $j=1, 2, \dots, M$ ）从顶点 $u_j$ 指向顶点 $v_j$ 。保证顶点 $N$ 可以从顶点 $1$ 到达。

初始时，所有边的权重均为 $0$ 。我们从 $M$ 条边中选择恰好 $K$ 条，将它们的权重修改为 $1$ 。请你求出在修改权重后的图中，从顶点 $1$ 到顶点 $N$ 的最短距离的最大值。

Constraints

$2 \leq N \leq 30$
$1 \leq K \leq M \leq 100$
$1 \leq u_j, v_j \leq N$
$u_j \neq v_j$
In the given graph, vertex $N$ is reachable from vertex $1$ .
All input values are integers.

思路

网络流是图论中的一类问题，研究如何在一个有向图中分配流量。图中的边有容量限制，流量不能超过容量。核心问题包括：

最大流问题：从源点 $s$ 到汇点 $t$ 的最大流量。
最小割问题：找到一组边，使得删除这些边后 $s$ 和 $t$ 不连通，且这些边的总容量最小。

Dinic 算法

Dinic 算法是求解最大流的高效算法，时间复杂度为 $O(V^2 E)$ ，核心步骤如下：

分层图：通过 BFS 构建从源点出发的分层图，记录每个节点的层级。
阻塞流：通过 DFS 在分层图上寻找增广路径，并更新剩余容量。

问题转换

最短距离的定义是路径上所有权重之和的最小值。我们需要选择 $K$ 条边设为 $1$ ，使得所有可能的路径中，权重之和的最小值尽可能大。这个问题可以通过二分答案解决：

假设答案为 $d$ ，需要验证是否存在一种选边方式，使得所有从 $1$ 到 $N$ 的路径的权重之和至少为 $d$ 。
若存在，尝试更大的 $d$ ；否则，尝试更小的 $d$ 。

网络流建模

为了验证某个 $d$ 是否可行，构造一个分层图，将问题转化为最大流问题：

分层图构造：
- 将每个顶点拆分为 $d$ 层，每层代表路径中的一个步骤。顶点 $u$ 在第 $k$ 层的节点编号为 $u + (k-1) \times N$ 。
- 对每条原图的边 $(u_j, v_j)$ $(u_{j}, v_{j})$ ，在第 $k$ $k$ 层添加两条边：
  - 层内边：从第 $k$ 层的 $u_j$ 指向第 $k$ 层的 $v_j$ ，容量为 $1$ （表示选中这条边）。
  - 跨层边：从第 $k$ 层的 $u_j$ 指向第 $k+1$ 层的 $v_j$ ，容量为极大值（如 $10^6$ ，表示不选中这条边）。
- 在每层末尾添加边：从当前层的 $N$ 指向下一层的 $N$ ，容量极大值（确保可以跨层到达终点）。
最大流的意义：
- 从第 $1$ 层的起点 $1$ 到第 $d$ 层的终点 $N \times d$ 的路径必须经过 $d$ 步。
- 每条路径中使用的层内边数量即为选中的边数量。最大流的值即为需要选中的边的最小数量。
- 若最大流 $\leq K$ ，则说明可以用 $\leq K$ 条边构造分层图，保证原图中所有路径的权重至少为 $d$ 。

二分答案

通过二分法确定最大的 $d$ ：

初始范围： $l = 0$ （最短距离下限）， $r = N-1$ （路径长度的上限）。
验证步骤：
1. 计算中点 $mid = \lfloor \frac{l + r + 1}{2} \rfloor$ 。
2. 构造分层图并计算最大流。
3. 若最大流 $\leq K$ ，则令 $l = mid$ ；否则令 $r = mid - 1$ 。

分层图示例

假设 $d = 2$ ，原图中有一条边 $(1, 2)$ 。分层图构造如下：

第 $1$ 层：顶点 $1$ 和 $2$ 。
第 $2$ 层：顶点 $3$ 和 $4$ （对应原顶点 $1$ 和 $2$ ）。
边 $(1, 2)$ 的处理：
- 层内边： $1 \rightarrow 2$ ，容量 $1$ 。
- 跨层边： $1 \rightarrow 4$ ，容量 $10^6$ 。

复杂度分析

二分次数： $\mathcal O(\log N)$ 。
每次 Dinic 的时间： $\mathcal O(d \times M)$ 。
总复杂度： $\mathcal O(d \times M \times \log N)$ ，在合理范围内。

总结

通过将问题转化为分层图的最大流问题，并利用二分法确定答案，可以在合理时间内求解最短距离的最大值。关键在于理解分层图的构造和网络流模型的建立，将原问题中的选边操作映射为网络中的流量限制。最终答案即为二分过程中找到的最大可行 $d$ 。

CODE

const int N = 2e5 + 10;

struct edge 
{
	int v;
	int w;
	int rev;
};

vector<edge> e[N];
int dis[N], iter[N];

void addEdge(int u, int v, int w)
{
	e[u].push_back(edge{v, w, (int)e[v].size()});
	e[v].push_back(edge{u, 0, (int)e[u].size() - 1});
}
 
void bfs(int s)
{
	queue<int> q;
	memset(dis, -1, sizeof(dis));
	dis[s] = 0;
	q.push(s);
	while (!q.empty())
	{
		int u = q.front();
		q.pop();
		for (int v = 0; v < (int)e[u].size(); v ++)
		{
			edge G = e[u][v];
			if (dis[G.v] == -1 && G.w)   
			{
				dis[G.v] = dis[u] + 1;
				q.push(G.v);
			}
		}
	}
}

int dfs(int s, int t, int f)
{
	if (s == t)
		return f;
	for (int &v = iter[s]; v < (int)e[s].size(); v ++)
	{
		edge &G = e[s][v];
		if (dis[G.v] == dis[s] + 1 && G.w)  
		{
			int d = dfs(G.v, t, min(G.w, f));
			if (d > 0)
			{
				G.w -= d;
				e[G.v][G.rev].w += d;
				return d;
			}
		}
	}
	return 0;
}

int Dinic(int s, int t)
{
	int ans = 0;
	while (1)
	{
		bfs(s);    
		if (dis[t] == -1)
			return ans;		
		int d;
		memset(iter, 0, sizeof(iter));          
		while ((d = dfs(s, t, inf)) > 0)  
			ans += d;
	}
	return ans;
}

void solve()
{
    int n, m, k;    cin >> n >> m >> k;
    vector<int> a(m + 1), b(m + 1);
    for (int i = 1; i <= m; i ++)
        cin >> a[i] >> b[i];

    auto chk = [&](int d) -> bool
    {
        for (int i=1;i<N;i++)   e[i].clear();
        for (int k = 1; k <= d; k ++)
        {
            for (int i = 1; i <= m; i ++)
            {
                addEdge(a[i] + (k - 1) * n, b[i] + (k - 1) * n, 1);
                addEdge(a[i] + (k - 1) * n, b[i] + k * n, 1e6);
            }
            addEdge(k * n, (k + 1) * n, 1e6);
        }
        int g = Dinic(1, d * n);
        return g <= k;
    };

    int l = 0, r = n - 1, mid;
    while (l < r)
    {
        mid = (l + r + 1) >> 1;
        if (chk(mid))   l = mid;
        else    r = mid - 1;
    }
    cout << l;
}

比赛题解

abc-397 题解

http://linyisu.github.io/2025/03/17/题解/2025-03-17-abc-397-题解/

作者

linyisu

发布于

2025年3月17日

许可协议

常系数齐次线性微分方程上一篇

可降阶的高阶微分方程下一篇