环形石子合并

石子合并 （链2）

题目描述

在一个圆形操场的四周摆放 $N$ 堆石子，现要将石子有次序地合并成一堆，规定每次只能选相邻的 $2$ 堆合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。

试设计出一个算法,计算出将 $N$ 堆石子合并成 $1$ 堆的最小得分和最大得分。

输入格式

数据的第 $1$ 行是正整数 $N$，表示有 $N$ 堆石子。

第 $2$ 行有 $N$ 个整数，第 $i$ 个整数 $a_i$ 表示第 $i$ 堆石子的个数。

输出格式

输出共 $2$ 行，第 $1$ 行为最小得分，第 $2$ 行为最大得分。

样例输入

4
4 5 9 4

样例输出

43
54

提示

$1\leq N\leq 100$，$0\leq a_i\leq 20$。

思路

该题是 合并石子 的进阶版，我们要思考如何运用其思路，解决本题。

首先，观察到，两题的区别体现在 链状 / 环状，且本题不仅需要求最小得分，还需要求得最大得分。

要想合并至只剩下一堆石子，就一定存在一个分界点，这个点左右两堆石子并不直接合并，而是通过其他石子的合并，最终合并在一起。

因此，可以考虑枚举这个分界点。

但是由于枚举分界点是 $\mathcal O(n)$ 复杂度，且 合并石子 的复杂度为 $\mathcal O(n^3)$ ，总的时间复杂度为 $\mathcal O(n^4)$ , 而 $1\leq N\leq 100$，则总计算量为 $100,\ 000,\ 000$, 可能超时。

接着想到，对于带有环的问题，一般考虑 化曲为直，因此将环斩为链，并在其后续上一段相同的链。

此时，当我们枚举 $i\in [1,\ n]$ 的长度为 $n$ 的区间，可以惊奇的发现，这些区间正好就是上面期望求得的 带有一个分界点的区间。

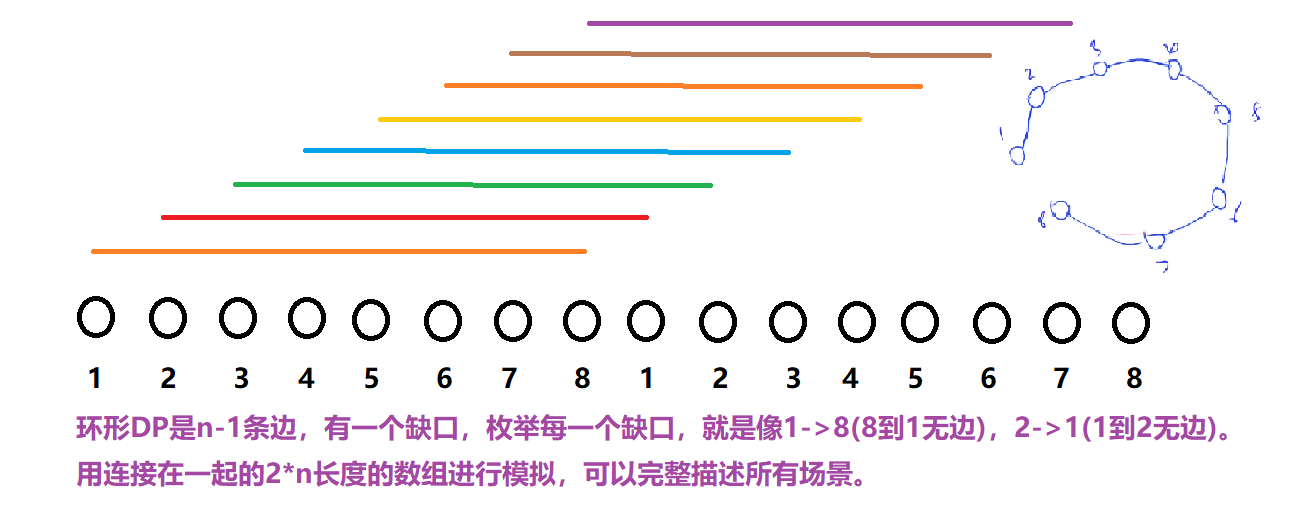
定义 $dp_{i\ j}$ 为将区间 $[i,\ j]$ 的石子合并成一堆的最小得分。

则可将 $[i,\ j]$ 区间通过一个分割点 $k$ 分为两个部分，问题转化为先合并分割点两端的小区间内的石子，进而将两堆石子合并。

因此，可以通过枚举 $k\ (k \in [i,\ j))$。

状态转移方程：

$f_{i\ j} = \mathop{min}\limits_{k\in[i,\ j-1]}\{f_{i\ k} + f_{k+1\ j} + \sum_{k=i}^{j-1}{v_i}\}$

$g_{i\ j} = \mathop{max}\limits_{k\in[i,\ j-1]}\{g_{i\ k} + g_{k+1\ j} + \sum_{k=i}^{j-1}{v_i}\}$

注意到递推式中存在 $\sum_{k=i}^{j-1}{v_i}$ 项，因此需要预处理前缀和。

同时，需要对 dp数组 初始化。

运用记忆化搜索，即可求得答案。

void solve()
{
    int n;  cin >> n;
    vector<int> v(2 * n + 1), pre(2 * n + 1, 0);
    vector<vector<int>> f(2 * n +1, vector<int>(2 * n + 1, inf));
    vector<vector<int>> g(2 * n + 1, vector<int>(2 * n + 1));
    for (int i=1;i<=n;i++)
    {
        cin >> v[i];
        v[i + n] = v[i];
    }
    for (int i=1;i<=2*n;i++)
        pre[i] = pre[i - 1] + v[i];

    auto work1 = [&](auto self, int l, int r) -> int
    {
        if (r - l + 1 == 1) return 0;
        if (f[l][r] != inf)    return f[l][r];
        
        for (int i=l;i<r;i++)
            f[l][r] = min(f[l][r], self(self, l, i) + self(self ,i + 1, r) + pre[r] - pre[l - 1]);
        return f[l][r];
    };

    auto work2 = [&](auto self, int l, int r) -> int
    {
        if (r - l + 1 == 1) return 0;
        if (g[l][r])   return g[l][r];

        for (int i=l;i<r;i++)
            g[l][r] = max(g[l][r], self(self, l, i) + self(self, i + 1, r) + pre[r] - pre[l - 1]);
        return g[l][r];
    };

    int mn = inf, mx = 0;
    for (int i=1;i<=n;i++)
    {
        mn = min(mn, work1(work1, i, i + n - 1));
        mx = max(mx, work2(work2, i, i + n - 1));
    }
    cout << mn << _endl << mx;
}