方格取数

方格取数【dp】

题目背景

NOIP 2000 提高组 T4

题目描述

设有 $N \times N$ 的方格图 $(N \le 9)$，我们将其中的某些方格中填入正整数，而其他的方格中则放入数字 $0$。如下图所示（见样例）:

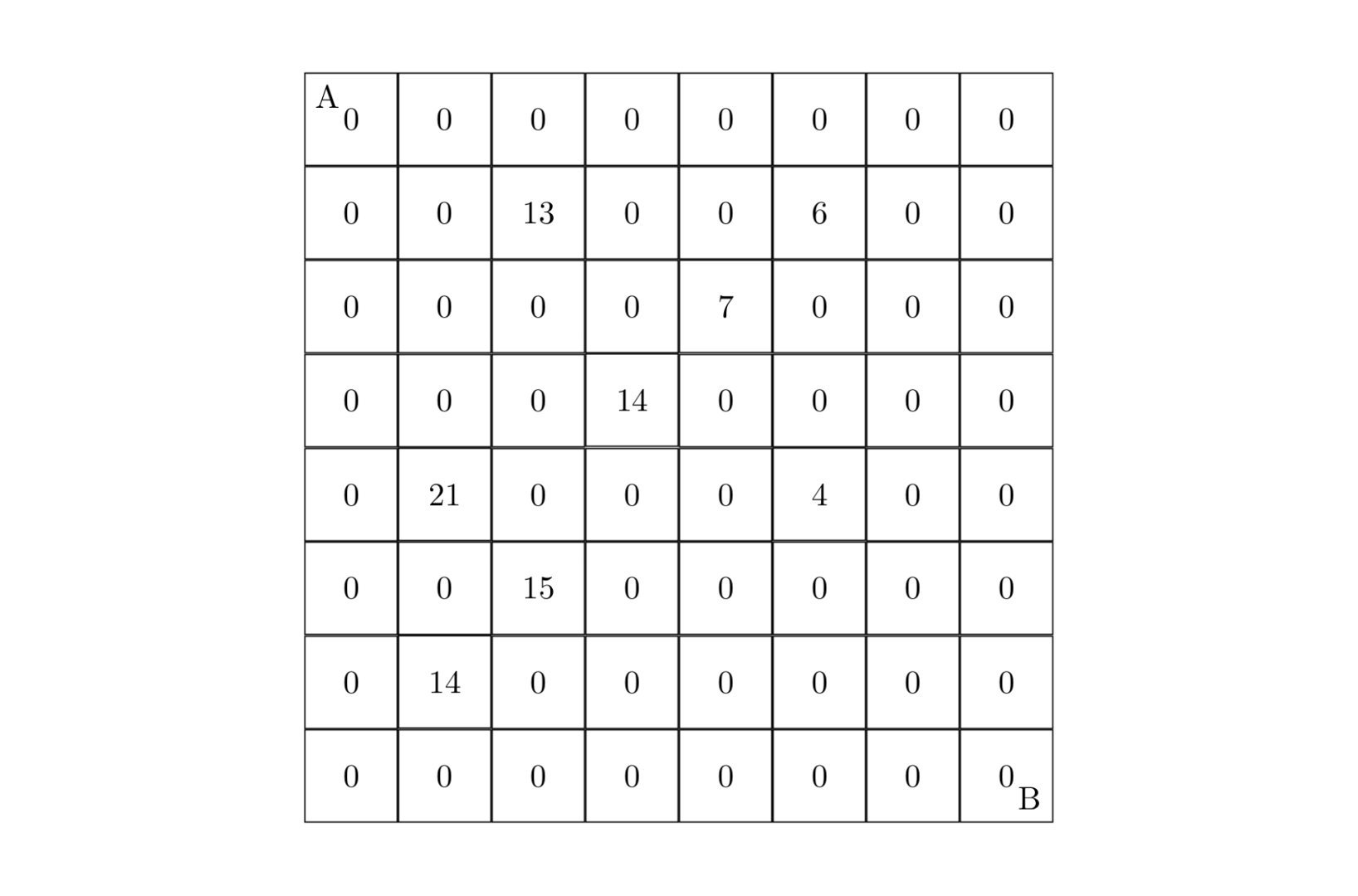
某人从图的左上角的 $A$ 点出发，可以向下行走，也可以向右走，直到到达右下角的 $B$ 点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字 $0$）。
此人从 $A$ 点到 $B$ 点共走两次，试找出 $2$ 条这样的路径，使得取得的数之和为最大。

输入格式

输入的第一行为一个整数 $N$（表示 $N \times N$ 的方格图），接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的 $0$ 表示输入结束。

输出格式

只需输出一个整数，表示 $2$ 条路径上取得的最大的和。

样例输入 #1

8
2 3 13
2 6  6
3 5  7
4 4 14
5 2 21
5 6  4
6 3 15
7 2 14
0 0  0

样例输出 #1

67

提示

数据范围：$1\le N\le 9$。

思路

如果记录完第一种方案，再计算第二种方案，不可控的因素太多了，大多都不是最优解，但两种方案同时执行就行，因为这可以根据当前的情况来判断最优。

因此就是四维动态规划。

定义状态 $f_{i\ j\ k\ l}$ 为从 $(1,1),\ (1,1)$ 分别走到 $(i, j),\ (k,l)$ 取得的数之和的最大值。

他的上一个状态可以有四种：

① 第一条路径从左来，第二条路经从左来

② 第一条路径从左来，第二条路经从上来

③ 第一条路径从上来，第二条路经从左来

④ 第一条路径从上来，第二条路经从上来

需要注意的是：当当前到的点重合时，说明第一次取过了，第二次到的时候应该是 $0$ , 因此不能算两次的 $v$ 。

转移方程：

$dp_{i\ j\ k\ l}=max\{dp_{i\ j-1\ k\ l-1},\ dp_{i\ j-1\ k-1\ l},\ dp_{i-1\ j\ k\ l-1},\ dp_{i-1\ j\ k-1\ l}\}+v_{i\ j} + v_{k\ l}$ $(i, j) \not= (k, l)$

$dp_{i\ j\ k\ l}=max\{dp_{i\ j-1\ k\ l-1},\ dp_{i\ j-1\ k-1\ l},\ dp_{i-1\ j\ k\ l-1},\ dp_{i-1\ j\ k-1\ l}\}+v_{i\ j}$ $(i, j) = (k, l)$

const int N = 15;
int v[N][N], dp[N][N][N][N];

void solve()
{
    int n;  cin >> n;
    int a, b, c, d;
    memset(v, 0, sizeof v);
    while (cin >> a >> b >> c, a || b || c)
        v[a][b] = c;
    for (int i=1;i<=n;i++)
        for (int j=1;j<=n;j++)
            for (int k=1;k<=n;k++)
                for (int l=1;l<=n;l++)
                {
                    int t = v[i][j] + (i == k && j == l ? 0 : v[k][l]);
                    a = dp[i][j - 1][k][l - 1];
                    b = dp[i][j - 1][k - 1][l];
                    c = dp[i - 1][j][k][l - 1];
                    d = dp[i - 1][j][k - 1][l];
                    dp[i][j][k][l] = max({a, b, c, d}) + t;
                }
    cout << dp[n][n][n][n];
}

在上面的代码中，我们可以发现，不是同步走到的格子方案是无效的，且观察到走过相同步数后，两条路径所到达的位置横纵坐标之和相等。利用这个性质，可以优化为三维动态规划。

定义状态 $f_{k\ i_1\ i_2}$ 为从 $(1,1),\ (1,1)$ 分别走到 $(i_1, k-i_1),\ (i_2,k-i_2)$ 取得的数之和的最大值。

状态和转移方程均保持不变。

$dp_{i\ j\ k\ l}=max\{dp_{i\ j-1\ k\ l-1},\ dp_{i\ j-1\ k-1\ l},\ dp_{i-1\ j\ k\ l-1},\ dp_{i-1\ j\ k-1\ l}\}+v_{i\ j} + v_{k\ l}$ $(i, j) \not= (k, l)$

$dp_{i\ j\ k\ l}=max\{dp_{i\ j-1\ k\ l-1},\ dp_{i\ j-1\ k-1\ l},\ dp_{i-1\ j\ k\ l-1},\ dp_{i-1\ j\ k-1\ l}\}+v_{i\ j}$ $(i, j) = (k, l)$

const int N = 15;
int v[N][N], dp[2 * N][N][N];

void solve()
{
    int n;  cin >> n;
    int a, b, c, d;
    memset(v, 0, sizeof v);
    while (cin >> a >> b >> c, a || b || c)
        v[a][b] = c;
    for (int k=2;k<=2*n;k++)
        for (int i1=1;i1<=n;i1++)
            for (int i2=1;i2<=n;i2++)
            {
                int j1 = k - i1, j2 = k - i2;
                if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
                {
                    int t = v[i1][j1] + (i1 == i2 ? 0 : v[i2][j2]);
                    a = dp[k - 1][i1 - 1][i2 - 1];
                    b = dp[k - 1][i1 - 1][i2];
                    c = dp[k - 1][i1][i2 - 1];
                    d = dp[k - 1][i1][i2];
                    dp[k][i1][i2] = max({a, b, c, d}) + t;
                }
            }
    cout << dp[2 * n][n][n];
}